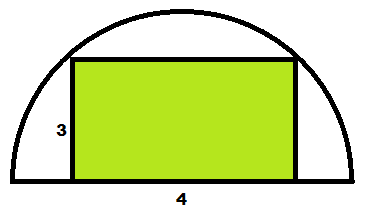
Um retângulo com lados de medidas 3 cm e 4 cm está inscrito em um semicírculo e tem um de seus maiores lados sobre o diâmetro do semicírculo.
A área do semicírculo, em centímetros quadrados, é
(A) $\displaystyle \frac{13\pi}{2} $
(B) $\displaystyle \frac{11\pi}{2} $
(C) $\displaystyle 5\pi $
(D) $\displaystyle \frac{7\pi}{2} $
(E) $\displaystyle 3\pi $
Resposta
Interpretando o problema
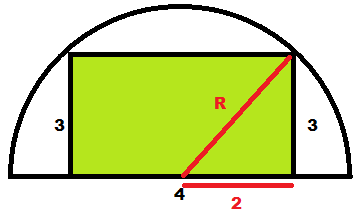
Note que Vamos calcular o raio utilizando o Teorema de Pitágoras
$\displaystyle R^2=3^2+2^2 $
$\displaystyle R^2=9+4 $
$\displaystyle R^2=13 $
$\displaystyle R=\sqrt{13} $
Agora podemos calcular a área do semicírculo
$\displaystyle A_{semicírculo}=\frac{\pi \cdot R^2}{2}$
$\displaystyle A_{semicírculo}=\frac{\pi \cdot (\sqrt{13})^2}{2}$
$\displaystyle A_{semicírculo}=\frac{13\pi }{2}$
Alternativa A






0 Comentários