
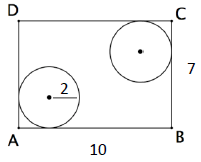
A figura a seguir mostra o retângulo ABCD onde AB=10 e BC = 7 e duas circunferências de raio igual a 2. As circunferências são tangentes a dois lados do retângulo.
A distância entre os centros dessas duas circunferências é
(A)$\displaystyle 5 \sqrt{2} $
(B)$\displaystyle 3 \sqrt{3} $
(C)$\displaystyle 4 \sqrt{3} $
(D)$\displaystyle 2 \sqrt{5} $
(E)$\displaystyle 3 \sqrt{5} $
Resposta.
Primeiro localizamos as informações na imagem
Depois note que a distancia dos centros é calculada a partir do Teorema de Pitágoras
$\displaystyle x^2 = 6^2 +3^2 $
$\displaystyle x^2 = 36 +9 $
$\displaystyle x^2 = 45 $
$\displaystyle x = \sqrt{45} $
$\displaystyle x = \sqrt{3^2 \cdot 5} $
$\displaystyle x = 3\cdot \sqrt{5} $
Alternativa E







0 Comentários